Lesson 16 - Response functions
Definition of response function
In our concentration on the detector side of our shielding problem, the ultimate goal
of this chapter is to reduce all of the data for a given detector into a single
flux-weighting function that can be used to get the detector response when used in an
equation of the form:
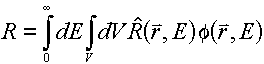
where 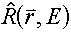 is
called the "response function", and has units of response/unit flux. This
form of the response function is not the most general, because it does not include angular
dependence that the text includes in Equation 5.6. This is because most detectors
are not directionally dependent. is
called the "response function", and has units of response/unit flux. This
form of the response function is not the most general, because it does not include angular
dependence that the text includes in Equation 5.6. This is because most detectors
are not directionally dependent.
Note: Generally, 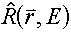 is a function and; is a function and; 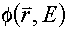 is a distribution. Therefore, their product is
a distribution with units of response/MeV/cc, which integrates to give response.
With this formalism, the flux can include Dirac deltas (which are distributions). (A
good example of this is the Dirac delta in energy that the uncollided flux
"inherits" from a monoenergetic source.) is a distribution. Therefore, their product is
a distribution with units of response/MeV/cc, which integrates to give response.
With this formalism, the flux can include Dirac deltas (which are distributions). (A
good example of this is the Dirac delta in energy that the uncollided flux
"inherits" from a monoenergetic source.)
With this mathematical form, we can create various simple response
functions.
Example 1: R = Total flux. For a desired
response equivalent to the total flux -- integrated over all space and all energies -- we
have:
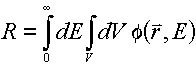
From which we must have 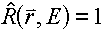 . .
Example 2: R = Total absorption. As an
example of a response equivalent to the total number of reactions of a given type, we
would have:
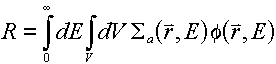
which gives us 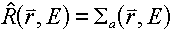 . .
Example 3: R = Thermal fission rate over a
sub-volume, 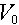 . As an
example of a partial response equivalent to the total number of reactions of a given type,
we would have: . As an
example of a partial response equivalent to the total number of reactions of a given type,
we would have:
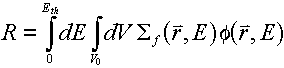
which gives us:
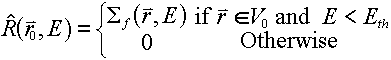 . .
Point response functions
In the previous mathematical form, the response function is a true
function. It is possible, mathematically, to create a point
response function using a combination of the Dirac delta function in space and a nominal
volume:
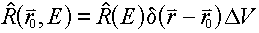
(The 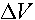 is
necessary to balance the units, since the Dirac delta would have units of per unit
volume.) is
necessary to balance the units, since the Dirac delta would have units of per unit
volume.)
In use, the basic equation changes to be energy only:
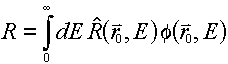
Relation of response function to cross sections
The response functions that are of interest to health physics are based on
the biological "response" of dose (i.e., energy deposition per unit mass) times
quality factor. The DOSE part of these response functions can be computed using our
knowledge of material properties of the medium that the detector is composed of. As
described in the text, the only piece of the puzzle that is needed to compute the response
function from cross sections is 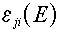 , which is the energy transfered to the material medium from
reaction type j of isotope i. Using this, the response function can be computed
from: , which is the energy transfered to the material medium from
reaction type j of isotope i. Using this, the response function can be computed
from:
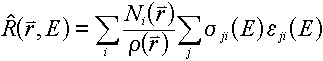
This response function is sensitive to the flux inside the detector; this
flux is, of course, is perturbed by the presence of the detector itself. We will
later relax this strict physical relationship in favor of an "point" response
function that is sensitive to the "unperturbed" flux that would exist if the
detector was not there. For the next couple of lessons, though, we will physically
tie the response function to material densities, cross sections, and fluxes associated
with a physical medium.
|
 NE406
Radiation Protection and Shielding
NE406
Radiation Protection and Shielding