Lesson 6 - General specifications of radiation sources
Types of sources
In this course, we will be working with four spatial layouts of sources. In this
lesson, we want to introduce them and get a little practice in converting from one type to
the other. The four are
- Point sources,
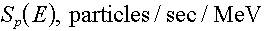
- Line sources,
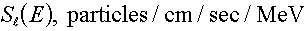
- Area (or surface) sources,
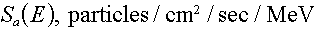
- Volumetric sources,
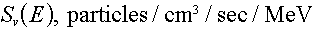
NOTE: Notice that I have simplified the notation somewhat from the
book, taking out the spatial and angular dependence. This is because we will be
dealing almost exclusively with uniform, isotropic sources.
Point sources,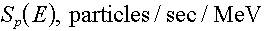
These are sources that denote particles that are spontaneously emitted from a single
point, with no physical source modeled:
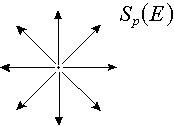
This is a mathematical simplification, of course, of a physical source. The book
gives two general requirements for assuming this:
- Volume of physical source sufficiently small in comparison with the dimensions between
source and detector; and
- Negligible interaction of radiation with the matter in the source volume.
and then states that Requirement 2 can be relaxed if source characteristics are
modified to account for source self-absorption. This relaxation is generally made by
performing a stand-alone calculation of a physical source, carefully collecting
information about the number and energy profile of particles (of all types) that escape
the source, and then attributing the escaping particles to the mathematical point source
in a subsequent calculation.
This allows the analyst to model the effects of the source without having to model the
source material in the calculation.
Line sources,
The line source, which has the addition dimension "per unit length," is a
similar mathematical simplification of a physical source, but one in which all
dimensions but one of the physical source are small in comparison with the
dimensions between source and detector. In other words, it is long and skinny
("pencil-like"). We call the dimension we keep the "length", L:
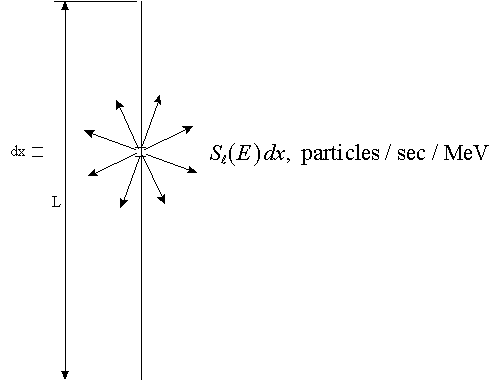
Notice that a differential length of the source emits 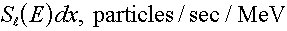 , therefore acts like a small point
source. The total particle emission rate from the line sources is  .
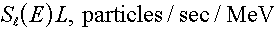NOTE: If one is given a line source and -- either
because you think the length is really not significant or just to be
conservative in your analysis or just to get an approximate answer to save time -- you can
reduce the line source to a point source with this strength. (You would probably
want to locate the point source at the midpoint of the line.)
Area (or surface) sources,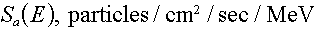
The analogy continues with the area source. If two dimensions cannot
be ignored, we model the source as a flat source and the dimension has a "per unit
area" in it. A differential area on the surface, then, acts like a
mini-point-source, and the total particle emission rate from the area source becomes  .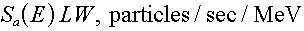
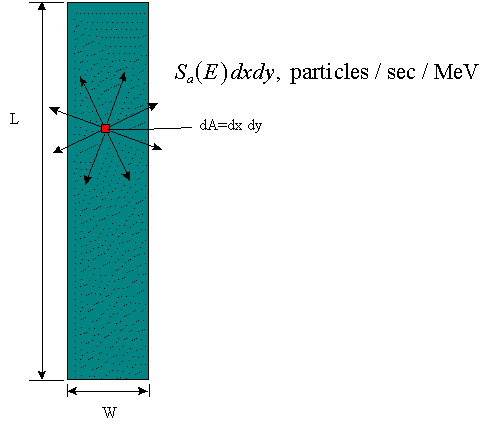
Example: In two dimensions, we have an additional
possibility for reducing the complexity of the source. For example, as the detector gets
further away from the surface, the analysis might first decide that the W dimension is no
longer significant but the L dimension is still significant; therefore,
the analyst might approximate the area source as a line source of length L (located, in
the figure, vertically centered left and right) with a strength
 .
Then, as the detector is withdrawn further and the analyst considers the L
dimension to be insignificant as well, the source might become a point source located at
the center of the originalsurface, with strength
 .
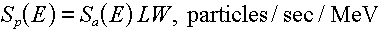Volumetric sources,
The final, and most general, form of the source that we will use is a full three
dimensional source, where all three spatial dimensions are significant. As an
example, consider as a parallelepiped (i.e., block) shaped source:
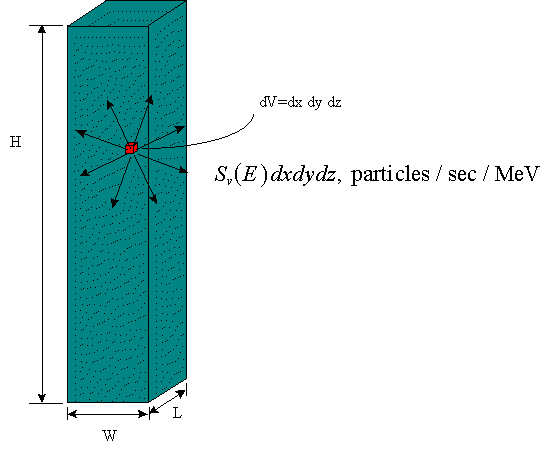
A volumetric source can also be reduced to the previous, simpler forms:
area source, line source, and point source. The exercise at the end of the lesson
will give you practice doing this.
Curie vs. Becquerel
The standard, preferred unit of activity is the Becquerel (Bq), which is 1
disintegration/sec. Us old guys still use the Curie (Ci), which is 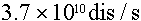 . You are caught in the middle
and have to know both.
Activity vs. particle production rate
Be sure to recognize the difference between these two. Sources are often
specified in terms of the disintegration rate of decaying isotopes; it is up to the
analyst to figure out the resulting particle source rate.
Appendix H in the book gives gamma and x-ray emission information for selected
radionuclides. This can be useful.
Example: What would be the source terms associated
with a 2 cm radius by 5 cm high cylindrical source of 90-day-old ruthenium-103 labeled as
having an activity 0.1 microcurie on a date 90 days ago?
Answer: From the Appendix H data, the half-life of Ru103
is 36.4 days, which gives us a decay constant of:
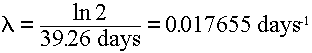
The current activity will be:
 
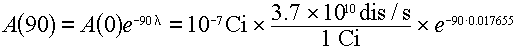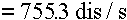
Since Ru-103 decays with release of a 497.1 keV photon 90.9% of the time
and a 610.3 keV photon 5.73% of the time, the associated total gamma production rate would
be:
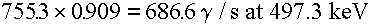
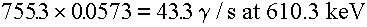
This would be the appropriate source strength if the source is represented
as a point source.
If the 62.83 cc volume of the source is modeled in the problem, then the
appropriate volumetric source terms are:
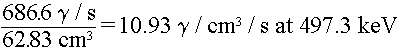
and
|
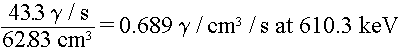
NE406
Radiation Protection and Shielding