Lesson 7: Interaction coefficients
In this lesson, we take concepts that you have already familiar from your previous
study of neutron cross sections and relate them to the slightly different notation
that is predominant in describing photon interactions. For this course, we need to
be familiar with both nomenclatures. In addition, this lesson describes the
scattering interaction coefficients in terms of distributions in energy and direction for
the particle after the scattering event.
Interaction coefficient = Macroscopic cross-section
In previous courses, you have learned the concept of the macroscopic cross section, 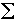 , for a material as the probability
of interaction per unit path, with units of , for a material as the probability
of interaction per unit path, with units of 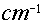 . For photons, the traditional symbol for this is . For photons, the traditional symbol for this is 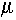 ; same idea, same unit. ; same idea, same unit.
Other variations that your are used to carry over to the new notation:
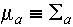 =
linear absorption coefficient (Not QUITE equivalent, but we will cover
the different in a later lesson) =
linear absorption coefficient (Not QUITE equivalent, but we will cover
the different in a later lesson)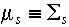 = linear scattering
coefficient = linear scattering
coefficient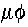 gives a collision rate in
interactions/cc/sec just like gives a collision rate in
interactions/cc/sec just like 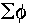 - a given
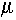 is associated with a
particle type and a particular material is associated with a
particle type and a particular material
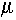 is
usually dependent on the energy of the particle, which is denoted as is
usually dependent on the energy of the particle, which is denoted as
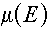 . .
Note: One notational convention that does not
carry over is that we do not use the subscript "t" on 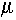 for "total". Instead, the "bare" for "total". Instead, the "bare" 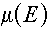 corresponds to the neutron notation
of macroscopic total cross section corresponds to the neutron notation
of macroscopic total cross section 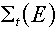 . .
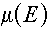 is referred to as the linear
attenuation coefficient, since it is the coefficient by which a photon
population decreases ("attenuates") as it penetrates a material (i.e., is referred to as the linear
attenuation coefficient, since it is the coefficient by which a photon
population decreases ("attenuates") as it penetrates a material (i.e., 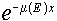 ). ).
Use of mass interaction and attenuation coefficients
One other convention that we will have to get used to is that the photon
interaction coefficients themselves are not usually tabulated (i.e., presented in data
tables or problem descriptions) as the 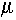 values we have discussed, but instead as this value divided
by the material density, values we have discussed, but instead as this value divided
by the material density, 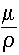 , which
has units of , which
has units of 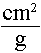 and is referred to
as the mass interaction (or attenuation) coefficients. (i.e.,The
word "linear" is replaced with the word "mass".) and is referred to
as the mass interaction (or attenuation) coefficients. (i.e.,The
word "linear" is replaced with the word "mass".)
This has been found to be useful for a number of reasons:
Where, as we have seen, the product of flux and linear interaction
coefficient, 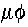 , gives us
interaction rate per unit volume, the product of flux and mass
interaction coefficient, , gives us
interaction rate per unit volume, the product of flux and mass
interaction coefficient, 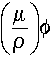 ,
gives us interaction rate per unit mass. ,
gives us interaction rate per unit mass.
As we will see in Chapter 5, the concept of dose, in
units of rad, is a measure of energy deposition per unit mass, which fits this unit
better..
For photons, 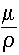 is often almost the same AT THE SAME ENERGY for different materials. (Water is the main exception.)
As we will see, photon interactions tend to be driven by the presence of electrons.
Since materials tend to have similar numbers of electrons/unit mass, this
uniformity results. is often almost the same AT THE SAME ENERGY for different materials. (Water is the main exception.)
As we will see, photon interactions tend to be driven by the presence of electrons.
Since materials tend to have similar numbers of electrons/unit mass, this
uniformity results. It really helps when your data is missing an element.
Note: It is somewhat surprising (to me, at least) to
compare the data in Tables C.5 on pages 451 and 452. It shows that the mass
interaction coefficients for air and water are very similar. (The principal
difference is that water has a substantial hydrogen content. Hydrogen delivers more
electrons per unit mass than any other element.)
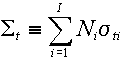
where I = number of isotopes
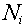 = number
density of isotope i (nuclei/barn/cm) = number
density of isotope i (nuclei/barn/cm)
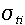 = microscopic
total cross section of isotope i (barns) = microscopic
total cross section of isotope i (barns)
No such juggling of units is
needed if we stay on a per mass basis, since:
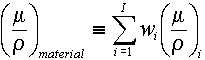
where 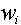 =mass
fraction of isotope i in the material =mass
fraction of isotope i in the material
|
 NE406
Radiation Protection and Shielding
NE406
Radiation Protection and Shielding